

WHIRLY DURLY LAB
12/3/21
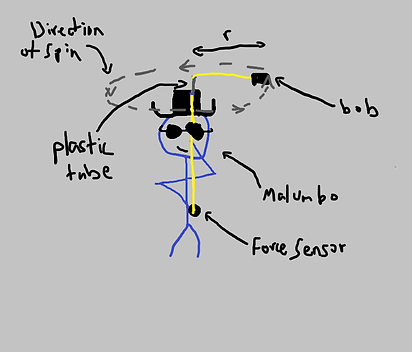
This is the Whirly Durly lab, a lab where we attached a weight onto a string and spun it around our head. We then measured the time it took this object to turn a specific amount of rotations at a given BPM, as well as the force of tension of the contraption at that BPM using a force sensor.
Overview
Research Question: 1. How does the speed of the contraption affect its acceleration?
Experiment:
Independent Variable: the Speed (Time Rotations) of the Whirly Durly.
Dependent Variable: the acceleration of the Whirly Durly.
Control Variable: the Radius of the Whirly Durly, as well as the Mass of the Whirly Durly.
The Controlled Variables
To keep the experiment controlled, we keep the total mass constant because an increase in mass would directly lead to an increase in inertia. We also keep the Radius, as a difference in Radius between measurements would influence the tangential speed of the Whirly Durly.
Meet The Team
Procedure
Experiment:
- We used a contraption with a 10 g weight attached to the end of a string, we also measured it to spin around with the radius of 60 cm.
- We spun the contraption around at different BPMs, starting with 130, 100, 75, 90, and 75.
- We measure the time it took for the contraption to spin 24 rotations, and collected the times using a phone stopwatch
- Simultaneously, we used a force sensor to record the force of tension acting on the contraption as we spun it.
- We repeated these steps for all 5 different BPMs recording the force in newtons and time in seconds.
- We then converted the raw data collected into the variables of angular speed (rpm), tangential speed (m/s), and acceleration (m/s^2).
Procedure
Raw Data

Whole .csv file is embedded below
Processed Data

To process the data we calculated the tangential speed (m/s) and the acceleration (m/s^2). the tangential speed (in meters/second) can be calculated by the angular speed (in radians/second) times radius (in meters). The tangential speed (in radians/second) can thus be calculated by rotations/time * 2pi * radius. Since we made revolved out measurements around 24 rotations of the Whirly Durly, the experiment will always have 24 rotations and a radius of 0.6m, thus we can get the tangential speed = 1.2pi*24/t where t is the time in seconds that it took to rotate the bob 20 times. The acceleration can be found with Newton's Second Law of acceleration = net force/mass. The mass of the bob is always 0.010 kg, therefore our equation for acceleration is net force/0.010.

The procesed data earlier translated into the graph above, realting the speed of the Whirly Durly to its acceleration.To find the fit for this data set, at first we tried a linear fit, but since this model suggested a non-zero y-intercept (meaning that if the Whirly Durly is spun at zero speed, it will have a nonzero acceleration) , it did not make sense and we had to look elsewhere. Then we tried a proportional fit to account for the non-zero acceleration problem. However, this suggests that when the speed is negative, which means to spin it in the opposite direction, I would have a negative acceleration. As the model suggests that the Whirly Durly would also accelerate away from the center of its path of rotation, while in reality it stayed in Michaels hands during the spin, the proportional model was, again, incorrect. Finally, we used a a simple quadratic model of y=Ax^2 to model our daata, which met both of the previous criteria mentioned above. The best-fitting equation we got was A = 1.703v^2. The slope of the graph is increasing as speed increases. This means that for every increase in speed, the acceleration increases by more and more.
Downloads of the two graphs are linked below
Processed Data
Conclusion
This lab helps us to prove the centripetal motion formula, ac = v^2/r. In the graph. We used the quadratic model a = Av^2, but this constant A of 1.703 is relatively close to 1.667, which is obtained by dividing 1 by the radius of the path 0.6. Doubling the radius of the path would lead to half the centripetal motion, while doubling the velocity would lead to quadruple the centripetal motion.
Centripetal acceleration occurs everywhere in our daily lives. When you turn a car around a corner, the car has centripetal acceleration. Instead of the force of tension in our experiment, the net force acting on the car would be the static friction force between its wheels and the ground. But due to the fact that the static friction keeping you turning also has a maximum threshold, once you exceed that threshold in some way (turning a tight corner too fast), the car's inertia tales over and you spin off the turn and the car looses control.
Uncertainties and Limitations
Experiment
The main source of uncertainty in this experiment was the range of the data. We couldn't spin the Whirly Durly too fast because that would be dangerous. Also if we spun the Whirly Durly too slowly, the thread would dangle and the radius would be less than 0.6m. As a result, we only had a limited amount of data. For each BPM, we simply completed one try. This makes the results unreliable since they could be influenced by a multitude of factors, including human errors in spinning, timing, and counting revolutions.
Improvements?
As with most experiments, a higher number of data and a larger data set wouldn't hurt. A safe environment where maximise the variation of data would also minimise the uncertainty of the experiment, where the Whirly Durly could be spun faster.

