

CIRCULAR MOTION
Circular motion is a movement of an object along the circumference of a circle or rotation along a circular path. It can be uniform, with constant angular rate of rotation and constant speed, or non-uniform with a changing rate of rotation. Examples of circular motion include: an artificial satellite orbiting the Earth at a constant height, a ceiling fan's blades rotating around a hub, a stone which is tied to a rope and is being swung in circles, or a car turning through a curve in a race track.
Terminology
Uniform Circular Motion - The motion of an object in a circle at a consistent speed is known as uniform circular motion.
Universal Gravitation - A way to interpret the strength of the gravitational field acting on an object outside of earth's domain, or is too far away to matter, as we cant use little g as a stable acceleration for Fg now. Calculated by the gravitational constant G (a quantity whose size depends on the system of units used and which is a universal constant) multiplied by the product of the masses (m1 and m2) and divided by the square of the distance R gives the magnitude of the attractive force F: F = G(m1m2)/R2.
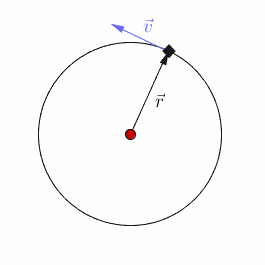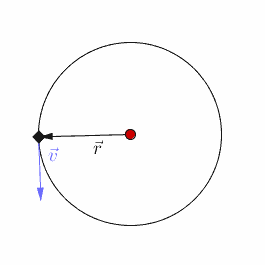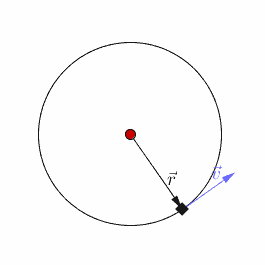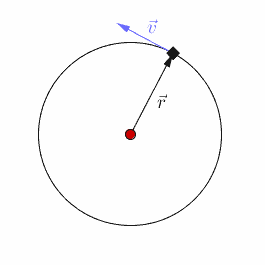
Uniform Circular Motion
The constant motion of an object in a circle is circular motion. When an object moves in a circle, its direction is continually changing. The object is always travelling in a tangent to the circle. The velocity vector is also tangent to the circle since the direction of the object's motion is the same as the direction of the velocity vector. A vector arrow is used to show this in the animation to the right. Circular motion is usually regarded in two terms: Angular and Tangential velocity. They differ greatly by what they measure, which can be demonstrated with an example.
Consider two items on a rotating disk, one near the disk's center and the other towards the disk's periphery. The angle is the only thing that matters when it comes to angular (rotation) speed. When the disk is spinning, how long does it take each object to move an angle of pi? They take the same amount of time, hence their angular speed is the same.
Consider the true speed of each object, though. The one farther out from the center must travel a greater distance to complete the circle in the same period of time as the one closer to the center, hence it is traveling quicker (tangential speed). Hence this is the difference between tangential and angular velocity.
Angular Velocity
The pace at which an item spins or circles around an axis, or the rate at which the angular displacement between two bodies varies, is referred to as angular velocity. Angles are commonly measured in radians, while angular velocities are measured in radians per second in mathematics and physics.
Angular velocity is most commonly referred to in the lowercase Greek letter Omega, ( the formula to obtain Omega, Angular velocity, is below ):
Tangential Velocity
The linear speed of any item travelling in a circular route is known as tangential velocity. At any point, the velocity of a body moving in a circular path at a distance r from the center is directed tangentially. Tangential velocity is the term for this. To put it another way, the linear velocity is equal to the tangential velocity at any given time.
Tangential velocity can be calculated as a using Omega ( angular velocity ) below:




Universal Gravitation
A way to interpret the strength of the gravitational field acting on an object outside of earth's domain, or is too far away to matter, as we cant use little g as a stable acceleration for Fg now. In 1798, Henry Cavendish conducted an experiment in which he precisely calculated the gravitational force between two objects. We now know that the gravitational force between two things is equal to the universal gravitational constant G (6.67*10^-11) times the mass of the first object divided by the distance between them squared. G(m1*m2)/r2 = Fg When one object's mass doubles, the gravitational pull between them likewise doubles. The gravitational force quarters as the radius between the two objects doubled.
Orbital Motion
According to field theory, an object creates a field that exists everywhere in space. The gravitational field of the Earth, tiny g, can be estimated using the formula g = Fg/m, where m is the mass of an object on Earth. Fg = G*m*mE/rE2, where mE is the mass of the Earth and rE is the distance between the Earth's centre and its surface, is derived from the universal gravity equation above. We get g = (G*m*mE)/rE2/m = G*mE/rE2 when we plug this back into the equation. mE is approximately 5.972*10^24 kg, while rE is approximately 6.38 * 10^6 m. We discover that g is equal to the well-known figure of 9.81 m/s^2.
Orbital Motion
This happens when an object moves ahead while being pulled towards another object by gravity. This is also depicted by the Newton's cannon experiment. The equations of universal gravitation and centripetal acceleration can be used to describe orbital motion. We know that net force = m*a because to Newton's Second Law. When an object orbits another object in space, it is only subjected to the gravitational force of the larger object. As a result, Fg = m1*a, where m1 is the object's mass. This is the same as Fg = m1*ac, where ac is the centripetal acceleration of the satellite. G*m1*m2/r2 = m1*v2/r, simplified to G*m2/r = v2, where m2 is the mass of the larger object, can be obtained by simplifying the equations of centripetal motion, which the planet exerts on the object. Because m1 cancels out in this equation, circular motion is independent of the mass of the satellite. Circular motion, on the other hand, is dependent on the satellite's speed. It must be close to the planet if it moves at a fast speed (a smaller radius). The satellite must be far away from the Earth if it travels slowly (a bigger radius). A link to the Newton's Cannon experiment can be found below (https://physics.weber.edu/schroeder/software/NewtonsCannon.html).





