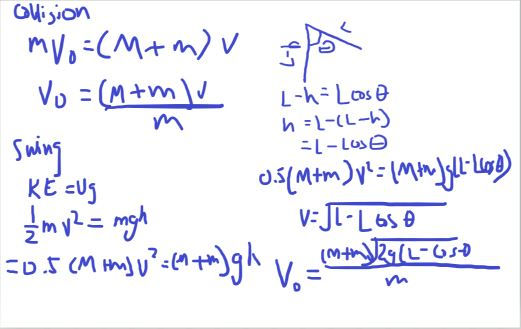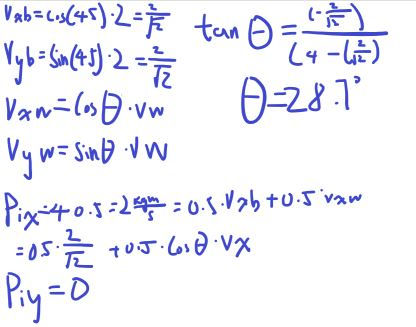
Momentum
The term "momentum" refers to "mass in motion." Because all objects have mass, if they are moving, they have momentum - their mass is moving. The amount of momentum that an object possesses is determined by two factors: the amount of material moving and the speed at which it is traveling.
Key Terms
- Momentum is a vector term in physics that represents "mass in motion." Mass*velocity = momentum (p). It can alternatively be translated as "the difficulty of stopping an object." In isolated systems with no external net force, momentum is conserved (no impulse).
- There must be an impulse in non-isolated systems, therefore ultimate momentum differs from initial momentum.
- Impulse: The impulse (J) is a force that acts over a period of time, and it is defined as J = F*t. We know that F = ma, so J = ma*t, and that a = v/t, so J = mv or J = p, the momentum change. As a result, F*t=p
Explosion: The conversion of potential energy to kinetic energy in a short period of time.
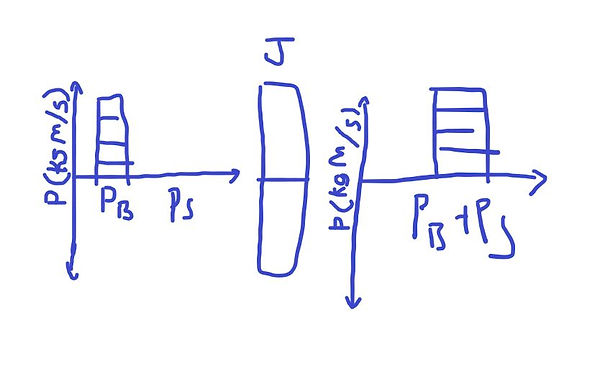
Representing Momentum Transfers with LIL Charts
We can use momentum bar charts or the LIL chart to illustrate momentum. The first L represents all of the system's beginning momentum, the I represents the impulse (negative/positive), and the last L represents all of the system's final momentum. Lets tackle a problem with this methodology.
A huge fish with a mass of 3m and a velocity of 2m/s eats a small fish with a mass of m at rest in this example. Because there is no net external force acting on this two-fish system, momentum is preserved. If we know this, we can use it to calculate the giant fish's final velocity after it eats the small fish:
Because there is no net external force acting on this two-fish system, momentum is preserved. If we know this, we can use it to calculate the giant fish's final velocity after it eats the small fish:

Force Time Graphs
Since Impulse is Force * Time, the area under a force time graph would be the Impulse.
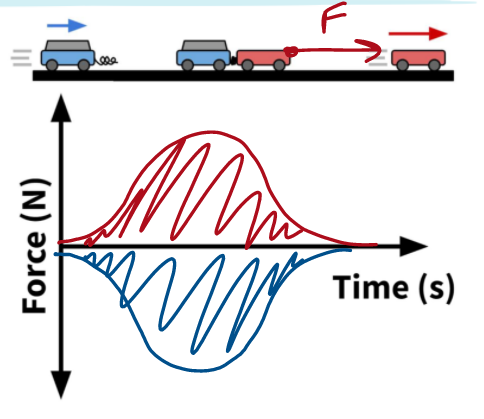
Consider this example: The two cars in this case have the same p since they are subjected to the same force (according to Newton's Third Law) and have the same contact time. The blue car's momentum is transferred to the red car. This situation is illustrated by the Force Time Graph below:
Another trick to remember is that instead of taking the integral of the function, finding the area under a Force Time Graph parabola can be as simple as multiplying the average force and time, illustrated below:

Collisions
There are 4 types of collisions:
Perfectly inelastic collisions (sticky): Perfectly inelastic collisions occur when two objects collide and meld into one. As a result of the deformation, kinetic energy is wasted.
Inelastic: The two items deform, but they do not become one. The kinetic energy is lost
Elastic: There is no deformation, therefore kinetic energy is conserved.
Explosions (super-elastic): Potential energy is converted to kinetic energy, and kinetic energy is increased.
However, momentum is conserved in each of those four scenarios. The momentum of the CENTER of MASS is unaffected by explosions.
Momentum Problem Solving
Consider this problem:
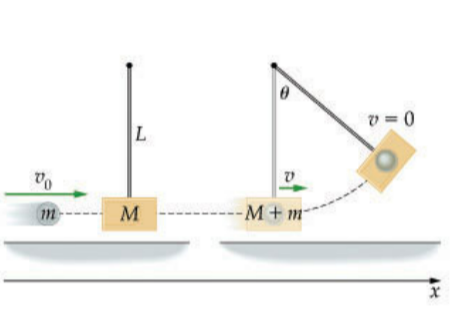
In a ballistic pendulum an object of mass mmm is fired with an initial speed v0 at a pendulum bob. The bob has a mass M, which is suspended by a rod of length L and negligible mass. After the collision, the pendulum and object stick together and swing to a maximum angular displacement θ as shown. Find an expression for v0, the initial speed of the fired object.
Consider this problem: